Get summaries, questions, answers, solutions, notes, extras, PDF and guide of Class 11 (first year) Economics textbook, chapter 5 Production Function AHSEC Class 11 Economics notes, which is part of the syllabus of students studying under AHSEC/ASSEB (Assam Board). These solutions, however, should only be treated as references and can be modified/changed.
If you notice any errors in the notes, please mention them in the comments
Summary
The chapter discusses the concept of production from the perspective of a producer, focusing on the relationship between inputs and output. The production function is introduced, which represents the relationship between physical inputs, like capital and labour, and the output. A key assumption made is that production is efficient, meaning that given certain inputs, a producer will achieve the maximum possible output. The chapter explains that technology plays a crucial role in determining how much output can be obtained from the same amount of inputs, and improvements in technology can change the production function.
The production function is a purely physical and technical relationship, which means it only concerns the quantities of inputs and outputs, without involving their monetary values. It is determined by the state of technology at a given time and expressed over a specific period, such as a day, week, or month.
The chapter then introduces two types of factors of production: fixed factors, like machines, which remain unchanged even if the output changes, and variable factors, like labour, which vary with the level of output. This distinction leads to a discussion of short-run and long-run production. In the short run, only some inputs can be adjusted, with others being fixed, while in the long run, all inputs can be varied.
In the short run, the relationship between a variable input, such as labour, and output is called the short-run production function. It assumes that one input is variable, while others, like capital, are fixed. For example, if a firm produces more chairs by hiring more workers while keeping the number of machines constant, this would illustrate a short-run production function. In the long run, however, all inputs, including both capital and labour, can be adjusted. The relationship in this case is called the long-run production function.
The chapter also discusses two types of production functions: short-run and long-run. In the short run, only one input can be varied, while the others remain constant. In the long run, all inputs can be changed simultaneously. For example, if a factory hires more workers and buys more machines, both factors are changed, which describes a long-run situation.
An important concept introduced in the chapter is the “isoquant,” which is similar to the “indifference curve” in consumer theory. An isoquant represents different combinations of inputs, like labour and capital, that produce the same level of output. The slope of the isoquant shows the rate at which one input can be substituted for another without changing the output. The chapter explains that the shape of the isoquant reflects diminishing returns, meaning that as more and more of one input is used, it becomes harder to substitute it for another without affecting the total output.
The chapter further delves into the different types of product: total product (TP), average product (AP), and marginal product (MP). Total product is the total output produced by a firm during a specific period, given certain inputs. Average product is the output per unit of input, and marginal product measures the additional output generated by using one more unit of the input. The chapter uses tables and examples to illustrate how these concepts change with different levels of input.
Lastly, the chapter introduces the Law of Variable Proportions. This law explains how changes in one input, while keeping other inputs constant, affect the output. Initially, increasing the variable input, like labour, increases the total product at an increasing rate, which is known as increasing returns. However, after a certain point, the total product starts to increase at a decreasing rate, indicating diminishing returns. If the input is increased further, the total product can even begin to decrease, leading to negative returns.
The chapter concludes by emphasizing the relationship between total product, average product, and marginal product. It explains that when the total product increases at an increasing rate, the marginal product also increases. When the total product grows at a decreasing rate, the marginal product decreases but remains positive. If the total product starts to fall, the marginal product becomes negative.
This chapter offers a foundational understanding of how producers behave, focusing on the production process, the role of inputs, and how output changes in response to different combinations of these inputs. The technical relationships outlined, such as the production function and the law of variable proportions, are central to the study of microeconomics and help in understanding the dynamics of production and efficiency in a firm.

Video tutorial
Textbook solutions
Very Short Answer Type Questions
1. What is meant by production?
Answer: The amount of output that is produced with given quantities of inputs and technology is called production.
2. List any three inputs used in production.
Answer: Three inputs used in production are:
- Labour
- Capital
- Land
3. What is production function?
Answer: Production function is a technological relationship between physical inputs used and physical output produced by the firm.
4. Define the term ‘total product’.
Answer: Total product refers to the total output of a good produced by a firm with the given inputs during a specified period of time.
5. Define the term ‘marginal product’.
Answer: Marginal product can be defined as the increase in total product when employment of the variable input is increased by one unit, keeping all other inputs constant.
6. What is meant by ‘average product’?
Answer: Average product (AP) is defined as the output per unit of variable input.
9. Can average product be zero or negative?
Answer: No, average product can never be zero or negative. It always remains positive.
10. Can marginal product be zero or negative?
Answer: Yes, marginal product can be zero as well as negative. It is zero when total product remains the same with an increase in variable input, and it is negative when total product falls with an increase in variable input.
11. Define the term ‘short run’ as used in production.
Answer: The short run refers to a period of time in which a firm can make changes only in the variable factors (like labour, raw materials), while fixed factors (like machinery, factory building) remain unchanged.
12. What do you mean by long run?
Answer: The long run is a period of time during which all factors of production can be varied.
13. What are fixed factors of production? Give examples.
Answer: Fixed factors of production are those factors which remain unchanged with the change in output. Examples include land, machinery, and buildings.
14. What are variable factors of production? Give examples.
Answer: Variable factors of production are those factors that vary with the level of output. Examples include labour, raw materials, and fuel.
15. Why does the MP curve cut the AP curve at its maximum point?
Answer: The MP curve cuts the AP curve at its maximum point because when AP rises, MP is above AP, and when AP falls, MP is below AP. Thus, MP equals AP at the highest point on the AP curve.
16. Define the term ‘returns to a factor’.
Answer: Returns to a factor refer to the change in output when only one input is increased, while all other inputs remain constant.
17. What is meant by increasing returns to a factor?
Answer: Increasing returns to a factor means that as more units of a variable factor are added to fixed factors, total output increases at an increasing rate.
18. State the law of diminishing returns to a factor.
Answer: The law of diminishing returns states that when additional units of a variable factor are applied to a fixed factor, after a certain point, the marginal product of the variable factor starts to decline.
19. The total product of a firm is 60 units when it uses 12 units of labour. Calculate the average product of labour. (AHSEC Question Bank)
Answer: AP = Total Product (TP) / Labour (L) = 60 / 12 = 5 units of labour
20. The total product of a firm is 70 units when it employs 10 units of labour. If the level of output increases to 75 units due to one unit increase in labour, find out the marginal product of labour. (AHSEC Question Bank)
Answer: MP = TP (new) – TP (old) = 75 – 70 = 5 units of labour
Short Answer Type Questions
1. Explain the concept of a production function. (NCERT)
Answer: The production function expresses the relationship between the quantities of inputs (factors of production) used and the quantity of output produced by a firm. It represents how output changes as the quantities of inputs are varied, keeping in mind the technological conditions under which the production takes place. The function shows the maximum output that can be produced with a given set of inputs.
2. Explain the concepts of short-run and the long-run. (NCERT)
Answer: In the short-run, at least one factor of production is fixed, and firms can change output only by varying the variable factors such as labour or raw materials. Capital, buildings, or machinery remain fixed in the short-run. In the long-run, all factors of production can be varied, and firms can adjust all inputs, including capital, land, and labour, to produce output. There are no fixed factors in the long-run.
3. Explain the relationship between the marginal products and total product of an input.
Answer: The relationship between the marginal product (MP) and total product (TP) of an input is as follows:
(i) When the MP of an input is increasing, the TP rises at an increasing rate. (ii) When the MP begins to decrease but remains positive, the TP continues to rise but at a decreasing rate. (iii) When the MP becomes zero, the TP reaches its maximum point. (iv) When the MP becomes negative, the TP starts to decline.
9. Explain the law of variable proportions in terms of the behaviour of total product.
Answer: The law of variable proportions shows the pattern of change in total output when only one input is increased, other inputs remaining unchanged. This law states that as we increase the quantity of only one input, keeping other inputs fixed, total product initially increases at an increasing rate, then at a decreasing rate, and finally at a negative rate.
10. Explain the law of variable proportions in terms of behaviour of marginal product.
Answer: The law of variable proportions in terms of marginal product behaviour states that initially, marginal product increases as the quantity of the variable input is increased. However, after a certain point, marginal product starts to decline but remains positive. Eventually, if the variable input continues to increase, marginal product becomes negative.
11. Can AP rise even when MP falls? Explain.
Answer: Yes, AP can rise even when MP falls. This happens when MP is greater than AP, which causes AP to increase even though MP is decreasing. AP will only start to fall when MP falls below AP.
12. Why does MP curve pass through the maximum point of AP curve?
Answer: The MP curve passes through the maximum point of the AP curve because when AP is rising, MP is greater than AP. When AP is at its maximum, MP is equal to AP. After that point, when AP starts falling, MP becomes less than AP.
13. Complete the following table:
| Units of Labour | AP (units) | MP (units) |
|---|---|---|
| 1 | 6 | 6 |
| 2 | 7 | ? |
| 3 | ? | 7 |
| 4 | 6.75 | ? |
| 5 | ? | 5 |
Answer: Let’s complete the missing values step by step:
- For the second row:
- We know the AP is 7 units and the MP is missing.
- AP = TP / L → TP = AP × L
- So, Total Product (TP) for 2 units of labour = 7 × 2 = 14
- MP for the second unit of labour = TP (with 2 units) – TP (with 1 unit) = 14 – 6 = 8
- For the third row:
- We know the MP is 7 and AP is missing.
- Total Product for 3 units of labour = TP (with 2 units) + MP = 14 + 7 = 21
- AP for the third unit of labour = TP / L = 21 / 3 = 7
- For the fourth row:
- We know the AP is 6.75 and the MP is missing.
- Total Product for 4 units of labour = AP × L = 6.75 × 4 = 27
- MP for the fourth unit of labour = TP (with 4 units) – TP (with 3 units) = 27 – 21 = 6
- For the fifth row:
- We know the MP is 5 and AP is missing.
- Total Product for 5 units of labour = TP (with 4 units) + MP = 27 + 5 = 32
- AP for the fifth unit of labour = TP / L = 32 / 5 = 6.2
Thus, the completed table is:
| Units of Labour | AP (units) | MP (units) |
|---|---|---|
| 1 | 6 | 6 |
| 2 | 7 | 8 |
| 3 | 7 | 7 |
| 4 | 6.75 | 6 |
| 5 | 6.2 | 5 |
14. State whether the following statements are true or false.
(i) If MP rises, AP must also rise.
Answer: True.
(ii) If MP falls, AP must also fall.
Answer: False.
(iii) If MP becomes negative, AP must also become negative.
Answer: False.
15. You are given the following input-output schedule:
| Units of variable input | Total output (in tonnes) |
|---|---|
| 5 | 50 |
| 10 | 100 |
| 15 | 125 |
| 20 | 140 |
| 25 | 145 |
(i) Calculate marginal product of the variable input:
The marginal product is calculated as the change in total output divided by the change in the number of units of the variable input. Here are the calculations:
- For 5 units to 10 units:
- Marginal product = (100 – 50) / (10 – 5) = 50 / 5 = 50
- For 10 units to 15 units:
- Marginal product = (125 – 100) / (15 – 10) = 25 / 5 = 25
- For 15 units to 20 units:
- Marginal product = (140 – 125) / (20 – 15) = 15 / 5 = 15
- For 20 units to 25 units:
- Marginal product = (145 – 140) / (25 – 20) = 5 / 5 = 5
Thus, the marginal product for each range of inputs is calculated as:
| Units of variable input | Total output (in tonnes) | Marginal product |
|---|---|---|
| 5 | 50 | 50 |
| 10 | 100 | 50 |
| 15 | 125 | 25 |
| 20 | 140 | 15 |
| 25 | 145 | 5 |
(ii) Calculate average product of the variable input:
The average product is calculated as the total output divided by the number of units of the variable input:
- For 5 units:
- Average product = 50 / 5 = 10
- For 10 units:
- Average product = 100 / 10 = 10
- For 15 units:
- Average product = 125 / 15 = 8.33
- For 20 units:
- Average product = 140 / 20 = 7
- For 25 units:
- Average product = 145 / 25 = 5.8
Thus, the average product for each number of input units is calculated as:
| Units of variable input | Total output (in tonnes) | Average product |
|---|---|---|
| 5 | 50 | 10 |
| 10 | 100 | 10 |
| 15 | 125 | 8.33 |
| 20 | 140 | 7 |
| 25 | 145 | 5.8 |
Long Answer Type Questions
1. Explain the notion of a production function. Distinguish between short run and long run production functions.
Answer: The production function shows the relationship between physical inputs and the physical output of a firm. It defines how much output can be produced with given quantities of inputs, assuming efficient production. A production function can be expressed as:
q = f(X₁, X₂, …, Xₙ), where q is the output and X₁, X₂, …, Xₙ represent different inputs.
The short run production function refers to a situation in which at least one input remains fixed, while other inputs can be varied. Typically, capital is considered fixed, and labour is the variable input. The output can be increased by increasing the variable input, while the fixed input remains unchanged. The short-run production function can be expressed as: q = f(L, K), where L is variable labour, and K is fixed capital.
In contrast, the long run production function refers to a situation in which all inputs are variable. Firms have the flexibility to adjust all factors of production. The output is determined by varying both inputs simultaneously in the same proportion. The long run production function can be expressed as: q = f(L, K), where both L (labour) and K (capital) are variable.
2. Explain the concepts of total product, average product and marginal product and show their relationship.
Answer:
- Total Product (TP): Total product refers to the total output produced by a firm using a given quantity of inputs during a specific period. For example, if 3 units of labour and a fixed amount of capital are used to produce 15 units of output, the total product is 15.
- Average Product (AP): Average product is defined as the output per unit of the variable input. It can be calculated as:
AP = TP / L
where L is the level of the variable input (labour) and TP is the total product. - Marginal Product (MP): Marginal product refers to the change in total product resulting from the employment of one additional unit of the variable input, keeping other inputs constant. It can be calculated as:
MP = ΔTP / ΔL
where ΔTP is the change in total product and ΔL is the change in the variable input (labour).
Relationship:
- When the marginal product is greater than the average product, the average product increases.
- When the marginal product is equal to the average product, the average product is at its maximum.
- When the marginal product is less than the average product, the average product decreases.
- The total product increases when the marginal product is positive. The total product is at its maximum when the marginal product becomes zero. After that, if the marginal product becomes negative, the total product decreases.
5. Explain the law of variable proportions. Use diagram.
Answer: The law of variable proportions shows the pattern of change in total output when only one input is increased, other inputs remaining unchanged. This law states that as we increase the quantity of only one input, keeping other inputs fixed, total product (TP) initially increases at an increasing rate, then at a decreasing rate, and finally at a negative rate.
This law outlines three stages of returns to a variable factor. These are:
(i) Increasing returns: When the marginal product (MP) of the variable factor rises, and the rate of change of output is greater than the rate of increase in the amount of variable factor. The TP increases at an increasing rate.
(ii) Diminishing returns: The marginal product of the variable factor starts declining, although TP increases but at a diminishing rate. At this point, TP continues to rise, but at a slower pace, and MP decreases but remains positive.
(iii) Negative returns: The marginal product of the variable factor becomes negative. In this stage, the TP curve slopes downwards, and MP falls below zero.
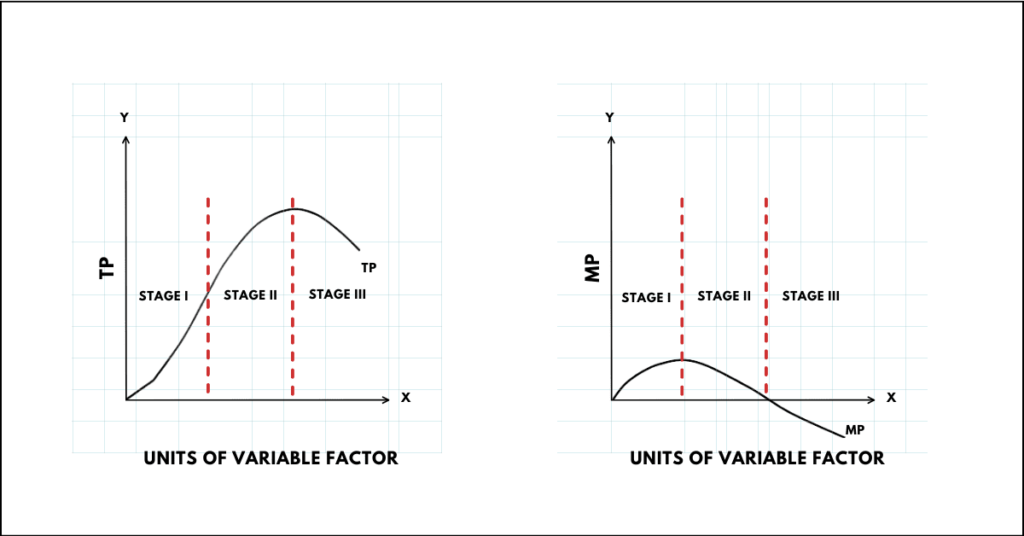
What is meant by returns to a factor? State the three phases of the law of variable proportions.
Answer: Returns to a factor refers to the change in output resulting from a change in the quantity of one input while keeping other inputs constant. The law of variable proportions explains the pattern of output as more units of a variable factor are employed with fixed factors. The three phases of the law are:
- Increasing Returns to a Factor: Total product increases at an increasing rate. Marginal product also rises.
- Diminishing Returns to a Factor: Total product increases at a diminishing rate, and the marginal product declines.
- Negative Returns to a Factor: Total product begins to decrease, and marginal product becomes negative.
6. To increase the production of a good, only one input is increased, while other inputs are held constant. Explain its effect on total product. Give reasons.
Answer: When only one input is increased, keeping other inputs constant, the effect on the total product follows the law of variable proportions:
- Initially, total product increases at an increasing rate due to better utilisation of fixed factors and the increasing efficiency of variable factors.
- As more units of the variable input are added, the total product increases at a decreasing rate due to the diminishing efficiency of the variable input in combination with the fixed input.
- Eventually, the total product starts to decrease if the variable input continues to increase, as the fixed factors become inadequate to support the additional variable input. This leads to overcrowding and inefficient use of resources.
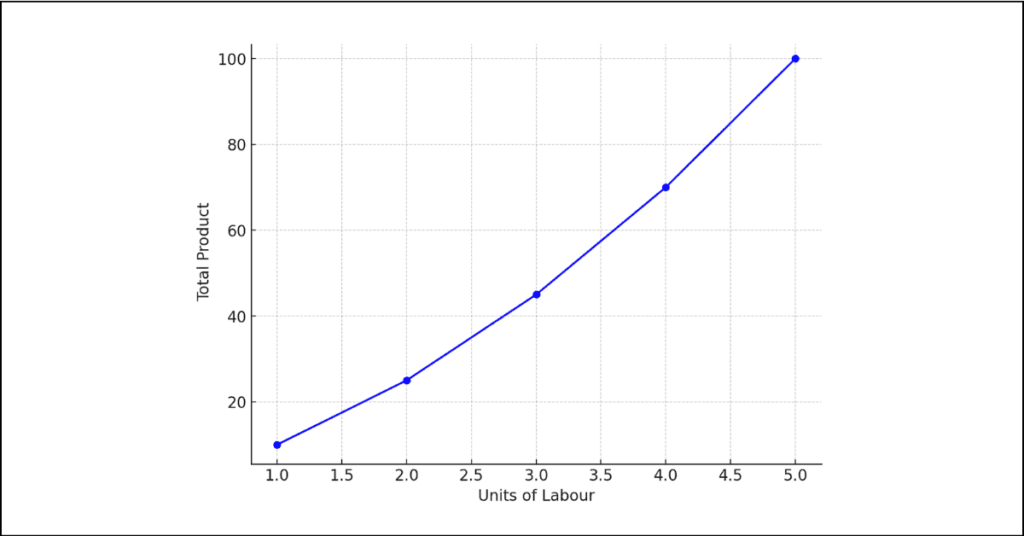
7. Explain the meaning of increasing returns to a factor with the help of a total physical product schedule and total physical product curve.
Answer: The law of increasing returns to a factor states that with a fixed amount of other factors of production, when more and more units of a variable factor are employed, total product increases at an increasing rate.
This can be explained with the help of a total physical product schedule and a total physical product curve.
Total Physical Product Schedule:
| Units of Labour | Total Product (TP) |
|---|---|
| 1 | 10 |
| 2 | 25 |
| 3 | 45 |
| 4 | 70 |
| 5 | 100 |
In the table, as the number of labour units increases, the total product increases at an increasing rate, indicating increasing returns to the variable factor of labour.
Total Physical Product Curve: In the total physical product curve, the number of labour units is shown on the x-axis, and the total product is shown on the y-axis. The curve rises steeply, showing that the total product is increasing at an increasing rate as more units of labour are employed.
8. What type of changes take place in total product and marginal product when there are
(a) increasing returns to a factor
(b) diminishing returns to a factor?
Why do these changes take place?
Answer: (a) When there are increasing returns to a factor, total product increases at an increasing rate, and marginal product also rises. These changes occur due to better utilisation of the fixed factor and increased efficiency of the variable factor.
(b) When there are diminishing returns to a factor, total product increases at a decreasing rate, and marginal product declines.
These changes happen because the fixed factor becomes inadequate relative to the variable factor, and the ideal factor proportion is disturbed.
9. Explain the law of variable proportions with the help of a total product schedule.
Answer: The law of variable proportions can be explained using the following total product schedule:
| Units of Labour | Total Product (TP) |
|---|---|
| 1 | 10 |
| 2 | 22 |
| 3 | 33 |
| 4 | 40 |
| 5 | 44 |
| 6 | 44 |
Initially, as labour increases from 1 to 3 units, total product increases at an increasing rate (from 10 to 33 units), indicating increasing returns. As labour increases from 3 to 5 units, total product increases at a decreasing rate (from 33 to 44 units), indicating diminishing returns. After the 5th unit, additional units of labour do not increase total product, and total product remains constant or may decline, showing negative returns.
Numerical Questions
1. The following table gives the MP of a factor. It is also known that the TP at zero level of employment is zero. Determine its TP and AP schedules.
Answer:
| Units of Factor Employment | MP | TP | AP |
|---|---|---|---|
| 1 | 20 | 20 | 20 |
| 2 | 22 | 42 | 21 |
| 3 | 18 | 60 | 20 |
| 4 | 16 | 76 | 19 |
| 5 | 14 | 90 | 18 |
| 6 | 6 | 96 | 16 |
Explanation:
- The Marginal Product (MP) is given in the question. Marginal product shows the additional output produced by employing one more unit of the factor.
- To calculate Total Product (TP), we add the marginal product of each successive unit of factor to the previous total. For instance:
- When 1 unit is employed, TP = 20 (from MP).
- When 2 units are employed, TP = 20 (previous TP) + 22 (MP for 2nd unit) = 42.
- This continues similarly for each unit.
- The Average Product (AP) is calculated by dividing the total product by the number of units of the factor employed:
- AP for 1 unit = TP / 1 = 20 / 1 = 20.
- AP for 2 units = TP / 2 = 42 / 2 = 21.
- And so on.
4. The production function of a production unit is given as: Q = 2L + 3K, where K = Capital and L = Labour.
(i) Find out the maximum level of output when L = 5 and K = 10.
(ii) Find out the maximum level of output when L = 6 and K = 0. (AHSEC Question Bank)
Answer:
(i) Maximum output when L = 5 and K = 10:
Q = 2L + 3K
Q = 2(5) + 3(10)
Q = 10 + 30 = 40 units.
(ii) Maximum output when L = 6 and K = 0:
Q = 2L + 3K
Q = 2(6) + 3(0)
Q = 12 + 0 = 12 units.
5. Let the production function of a firm be given as: Q = 5K²L², where K = Capital and L = Labour.
(i) Find out the level of output when K = 0 and L = 6.
(ii) Find out the level of output when K = 2 and L = 3. (AHSEC Question Bank)
Answer:
(i) Level of output when K = 0 and L = 6:
Q = 5K²L²
Q = 5(0)²(6)² = 5 × 0 × 36 = 0 units.
(ii) Level of output when K = 2 and L = 3:
Q = 5K²L²
Q = 5(2)²(3)² = 5 × 4 × 9 = 5 × 36 = 180 units.
Extra/additional questions and answers
Coming soon

Get notes of other boards, classes, and subjects
